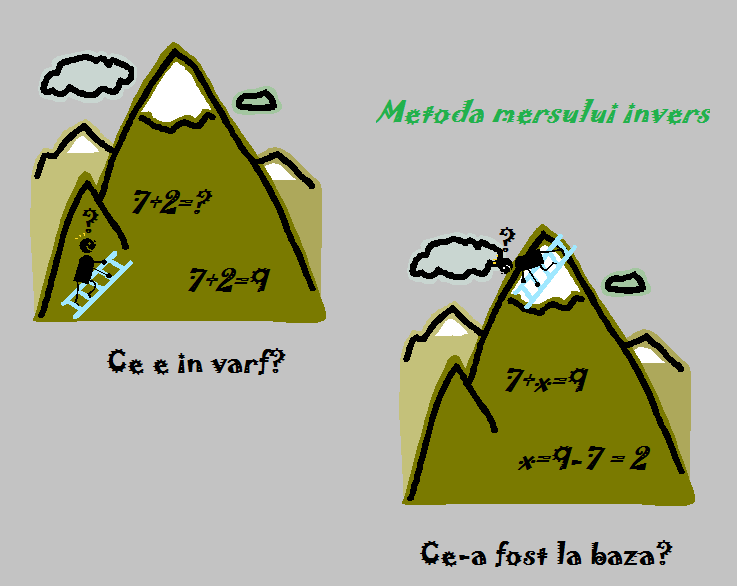
Metoda mersului invers = este acea metoda matematica in care rezolvarea exercitiului / problemei se face de la sfarsit (sau rezultat) catre inceput.
Aceasta nu este o metoda grea pentru copil, dar este o metoda care-l face sa greseasca foarte des, din neatentie (v-am povestit cum am scos-o la cap cu ecuatiile complexe, cu necunoscuta X, care se rezolva pe baza acestui principiu).
Acum m-am gandit sa scriu putin si despre problemele care se rezolva in acest mod si bineinteles nu "orsice", am ales problemele care se rezolva prin metoda figurativa + metoda mersului invers + niste fractii.
Dupa cum v-am mai spus mie imi plac lectiile presarate cu glume si asociatii haioase de aceea cred ca aceasta metoda poate fi inteleasa mult mai bine de copil, daca o asociem cu mersul pe:
- un munte - atunci cand se merge invers pe un munte inseamna sa cobori nu tot sa urci.
Dar puteti folosi si alte asociatii, de exemplu, decolarea avionului vs. aterizarea lui, dezbracarea unei rochite a unei papusi vs imbracarea ei etc..
Motivul asocierii este fixarea in capusorul copilului a faptului ca nu repetam operatiile din exercitiu sau problema, adica:
- daca intr-un exercitiu avem "+", atunci cand rezolvam invers vom avea "-" (prilej de a vorbi despre schimbarea semnelor daca doriti desi ea se va invata mai tarziu in gimnaziu).
- parantezele se rezolva invers nu mai incepem cu cea rotunda vom desfiinta intai acolada si apoi paranteza dreapta si la sfarsit parantezele rotunde.
- daca discutam despre un traseu vom analiza situatia de la punctul de sosire spre pornire si vom calcula lungimea acestuia etc.
Dupa ce le-am facut copiilor aceste precizari, sansele de aparitie al eventualelor greseli din neatentie (sau nestiinta) se vor diminua considerabil.
Dar cum matematica inseamna exercitii si probleme nu "vorbarie", iata niste exemple rezolvate:
Exemplul 1
"Cristina a primit o cutie de bomboane de la parintii sai. In prima zi a mancat impreuna cu prietene sale jumatate din bomboane, a doua zi a mancat 1/4 din bomboanele ramase, iar a treia zi jumatate din noul rest. Stiind ca in a patra zi a mancat ultimele 3 bomboane din cutie, afla cate bomboane erau in cutie." (Matematica, Culegere de exercitii si probleme pentru clasa a IV-a, Editura Aramis, Mariana Mogos si Stefan Pacearca)
Rezolvare:
Pasul 1 - desenul
VAR. A - desenul din aproape in aproape (daca vrei forma finala, sari peste explicatii, pana la Rezumat Var.A). In cazul desenului pornesc de la inceput catre sfarsit cu primele date.
- Desenez un segment care reprezinta cutia de bomboane (recomand foaie de matematica pentru usurarea reprezentarii grafice)
- apoi il impart in doua - bomboanele mancate in prima zi sunt jumatate (1/2) din toata cantitatea
- continui si impart in patru segmentul care reprezinta bomboanele ramase
- iau 1/4 din bomboanele ramase - adica bomboanele mancate in a doua zi
- impart in jumatate "noul rest" ( am sters vechile liniute care imparteau segmentul ramas in trei si l-am reimpartit in doua)
- reprezint pe desen ca s-au mancat jumatate din ele
- reprezint pe desen ca in ziua a patra s-au consumat ultimele 3 bomboane
Rezumat Var. A
Pentru desenul final, pe baza caruia voi calcula bomboanele din cutie, voi apela la notatii diferite pentru a nu se amesteca informatiile si le voi grupa pe toate.
Var.B
Inainte de a trece la rezolvarea problemei vreau sa mai fac un alt tip de desen.
(Am pastrat tipurile de linii de mai sus pentru a arata cosrespondenta si a prezenta doar varianta finala.)
Principala diferenta dintre cele doua desene este scoaterea restului si desenarea separata a ceea ce se intampla cu fiecare rest in parte.
Pentru tipul de problema exemplificat mai sus nu este obligatoriu un asemenea detaliu, dar sunt alte tipuri de probleme in care restul sufera modificari si atunci scoaterea lui permite un control crescut aspura tuturor datelor problemei (vezi problema urmatoare).
Pasul 2 - Rezolvarea
In cazul rezolvarii pornesc de la sfarsit catre inceput si cu ajutorul desenului de la varianta 2 (mi se pare mie mai clar) urmaresc parcurgerea datelor problemei.
(fac corespondenta dintre ziua 4 si ziua 3)
3 bomboane = 1/2 din bomboanele din ziua a 3-a
Ziua 3 -> 3 + 3 = 6 bomboane
(fac corespondenta dintre ziua 3 si ziua 2)
6 bomboane = 3/4 din bomboanele din ziua a 2-a
3 segmente = 6 => 1 segment = 6 : 3 = 2
2 bomboane = 1/4 din bomboanele din ziua a 2-a
Ziua 2 -> 6 + 2 = 8 bomboane
(fac corespondenta dintre ziua 2 si prima zi)
8 bomboane = 1/2 din totalul bomboanelor
Ziua 1 -> 8 + 8 = 16 bomboane ( totalul bomboanelor din cutia de bomboane)
R: 16 bomboane
|
Cate bomboane a mancat Cristina a treia zi?
1/2 = 3 bomboane (un numar egal cu bomboanele ramase)
Cate bomboane a mancat Cristina a doua zi?
6 = 3/4 = 3 segmente
|
Verificare (pentru a efectua aceste verificari copilul trebuie sa stie ca expresia o fractie dintr-un numar, adica a/b din y, este egala cu fractia inmultita cu acel numar, adica a/b x y, adica ay/b)
16 - 1/2 din 16 = 16 - 1/2 x 16 = 16 - 16/2 = 16 - 8 = 8
8 - 1/4 din 8 = 8 - 1/4 x 8 = 8 - 8/4 = 8 - 2 = 6
6 - 1/2 din 6 = 6 - 1/2 x 6 = 6 - 6/2 = 6 - 3 = 3 bomboane ramase
Exemplul 2:
"Ana, Daniel si Aurel au consumat caise dintr-o punga astfel: Ana cu 3 caise mai putin decat 1/3 din numarul total, Daniel cu 2 caise mai putin decat 1/3 din rest, iar Aurel cu o caisa mai putin decat 1/3 din ultimul rest .
Stiind ca in punga au mai ramas 9 caise, afla:a) Cate caise au fost la inceput in punga;
b) Cate caise a mancat fiecare copil."
(Matematica, Culegere de exercitii si probleme pentru clasa a IV-a, Editura Aramis, Mariana Mogos si Stefan Pacearca)
9 = numarul de caise ramase
9 = 2/3 + 1 -> 2/3 = 9-1 = 8
daca 2 segmente = 8 -> 1segment = 8 : 2 = 4 caise
Aurel a mancat cu o caisa mai putin decat 1/3
4 - 1 = 3 caise a mancat Aurel
segmentul verde (caisele ramase inainte de a lua Aurel) reprezinta:
4 x 3 = 12 caise (adica 1 segment x 3)
sau 9 + 3 = 12 caise (adica caisele ramase + cele mancate de Aurel)
12 = 2/3 + 2 -> 2/3 = 12 - 2 = 10
daca 2 segmente = 10 -> 1segment = 10 : 2 = 5 caise
Daniel a mancat cu 2 caise mai putin decat 1/3 din rest
5 - 2 = 3 caise a mancat Daniel
segmentul albastru (caisele ramase inainte de a lua Daniel) reprezinta:
5 x 3 = 15 caise (adica 1 segment x 3)
sau 9 + 3 + 3 = 12 + 3 = 15 caise (adica caisele ramase + cele mancate de Aurel + cele mancate de
Daniel)
15 = 2/3 + 3 -> 2/3 = 15 - 3 = 12
daca 2 segmente = 12 -> 1segment = 12 : 2 = 6 caise
Ana a mancat cu 3 caise mai putin decat 1/3 din numarul total
6 - 3 = 3 caise a mancat Ana
segmentul visiniu (punga cu caise) reprezinta:
6 x 3 = 18 caise (adica 1 segment x 3)
sau 9 + 3 + 3 + 3 = 12 + 3 + 3 = 15 + 3 =18 caise in total
(adica caisele ramase + cele mancate de Aurel + cele mancate de Daniel + cele mancate de Ana)
R:
la inceput in punga au fost 18 caise
Ana a mancat 3 caise
Daniel a mancat 3 caise
Aurel a mancat 3 caise
Verificare:
18 - 1/3 din 18 + 3 = 18 - 1/3 x 18 + 3 = 18 - 18/3 + 3 = 18 - 6 + 3 = 12 + 3 = 15
15 - 1/3 din 15 + 2 = 15 - 1/3 x 15 + 2 = 15 - 15/3 + 2 = 15 - 5 + 2 = 10 + 2 = 12
12 - 1/3 din 12 + 1 = 12 - 1/3 x 12 + 1 = 12 - 12/3 + 1 = 12 - 4 + 1 = 8 + 1 = 9 caise ramase
Precizare: Nivelul acestor probleme depaseste programa scolara pentru clasa a IV-a, parcursa la nivelul clasei, si se adreseaza copiilor care doresc sa stie mai mult si sa participe la concursuri scolare si mai tarziu la olimpiade de matematica.
Spor la treaba si rabdare!
***
Raspuns catre un cititor - rezolvare problema comentariu 1
In primul rand desenul eu il realizez in doi pasi: pasul 1 reprezint cat a citit Andreea in prima zi (1/8 +5) si pasul 2 cat a citit in ziua 2 si 3.
(Rezolvarea porneste de la sfarsitul desenului catre inceput)
3 segmente = 175 + 5 = 180 pagini (desenul 2)
1 segment = 180 : 3 = 60 pagini,
Cate pagini a citit Andreea in ziua 2?
60+5 = 65 pagini
Cate pagini a citit Andreea in ziua 2 si 3?
60+180=240 pagini
7 segmente = 240 + 5 = 245 pagini (desenul 1)
1 segment = 245 : 7 = 35 pagini
Cate pagini a citit Andreea in prima zi?
35+5=40 pagini
Cate pagini are cartea ?
175+65+40=280 pagini
Eu nu stiu care este metoda doamnei invatatoare. Daca s-a lucrat la clasa si cu intrebari de genul "Cate pagini reprezinta 7 sau 3 segmente?" pentru copilul meu doamna nu era asa stricta, important era desenul si rationamentul.










13 comentarii:
Am si eu o problema care nu o stiu rezolva,andreea citeste o carte in trei zile,in prima zi citeste o optime si 5 pagini,a doua zi citeste o patrime si 5 pagini,iar a treia zi citeste restul adica 175.cate pagini are cartea?doamna invatatoare vrea si desen si intrebari altfel nu ie bine tema
Raspunsul il gasiti mai sus, la sfarsitul postarii deoarece nu am putut realiza desenul la comentarii.
Din cate stiu si o povestit fetita doamna invatatoare nu a facut probleme de genu in clasa,doar cu metodele mai simple si fetita o zis ca o stat si s-o gandit oare cum sa rezolve problema si cum dansa nu o stiut le-o dato la copi acasa tema.va multumesc pt ajutor
Buna ziua. Va rog din suflet sa ma ajutati in rezolvarea unei probleme de cl a 4 a .Ionut are 19 ani iar mama sa 51. Cu cati ani in urma, varsta mamei a fost de 5 ori mai mare? Se poate rezolva prin metoda figurativa? Va multumesc
Se poate rezolva prin metoda grafica. Astfel de rezolvari gasiti in postarea ”Metoda figurativa - Metoda grafica - Metoda segmentelor”. Totusi o voi prezenta rapid aici:
- desenul corect este
/----/----/----/----/----/.../ 5 segmente pentru varsta mamei + un segment pe care trebuie sa-l aflam, adica perioada care a trecut
/----/.../ pentru Ionut 1 segment + aceeasi perioada, deoarece anii trec pentru amandoi
- desenul il voi alinia la stanga pentru a se vedea rezolvarea, dar corect se aliniaza in partea dreapta
/.../----/----/----/----/----/ 51 ani - mama
/.../----/ 19 ani - Ionut
Din desen se observa ca exista o parte comuna /.../----/, raman 4 segmente care sunt echivalente cu diferenta de varsta dintre cei doi
4s = 51-19=32
1s = 8
/..x./----/ 19
x+8=19 rezulta x=11 ani
Verificare:
5s+11=51, 40+11=51 adevarat
40:5=8 adevarat
Antonia are in pusculita o suma de bani. In prima zi cheltuie 2/3 din suma, a treia zi 3/4 din rest, a patra zi 4/5 din rest iar a cincea zi 5/6 din rest si ii mai ramane 1 leu. Cati bani a avut la inceput?
Multumesc pentru ajutor
Buna ziua, poate cineva sa ma ajute la problema de mai sus?
Multumesc.
Se deseneaza astfel:
Ziua 1) - un segment impartit in trei
Ziua 2) - ??? nu spune nimic problema
Ziua 3) - ultimul segment de mai sus se imparte in patru
Ziua 4) - ultimul segment de la ziua anterioara se imparte in 5
Ziua 5) - ultimul segment de la ziua anterioara se imparte in 6
Nu pot face tot desenul aici asa ca o sa scriu doar rezolvarea pe baza desenului de la fiecare pas (zi)
ziua 5
/---/---/---/---/---/.1 leu/ - la inceputul zilei 5 erau 6 lei
ziua 4
/----/----/----/----/..6lei./ - la inceputul zilei 4 erau 30 lei
ziua 3
/-----/-----/-----/...30 lei/ - la inceputul zilei 3 erau 120 lei
ziua 2 - ???
ziua 1
/------/------/....120 lei./ - la inceput au fost 360 lei
Copilul va trebui sa scrie operatiile matematice pentru a se vedea cum a ajuns la aceste valori.
Numai bine!
Multumesc frumos.
Bună ziua am și eu o problemă cu metoda mersului invers. Clasa a 4a. Copiii și din clasa a 4 a au pictat globuri pentru brad astfel:o treime din total, roșii; și două cincimi din rest,aurii; o jumătate din noul rest,verzi, și restul de 6 globuri, albastre. Câte globuri sunt în total și câte sunt de fiecare culoare?
Buna,am o problema : fie 7a+9b+2c si a+b=43 , b+c=15 sa se afle a, b, c. Am gasit factorul comun b si am rezolvat astfel: a=43-b si c=15-b, acum pot inlocui in ecuatia de baza 7(43-b)+9b+2(15-b)=301-7b+9b+30-2b. si de aici nu mai merge. Am gresit undeva? Am nevoie de ajutor. Multumesc
301-7b+9b+30-2b
301+2b+30-2b
2b-2b=o
=>=301+30
=331
Trimiteți un comentariu
Pe acest blog vor fi afisate doar comentariile care folosesc un limbaj adecvat si au legatura cu subiectele prezentate.